Huygens Erklärung des Brechungsgesetzes aufgrund seiner Wellenvorstellung

aus: Christian Huygens, Abhandlung über das Licht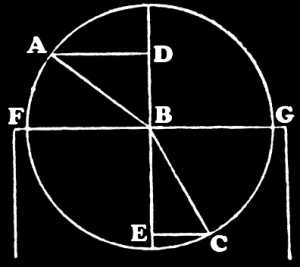

Wir wollen jetzt zur Erklärung der Brechungserscheiuungen übergehen. Wir machen dabei wie oben die Annahme, dass die Lichtwellen durch die durchsichtigen Körper hindurchgehen und hierbei eine Verminderung ihrer Geschwindigkeit erleiden.

Die hauptsächlichste Eigenschaft der Lichtbrechung besteht darin, dass ein Lichtstrahl, wie AB, der durch die Luft geht und schräg auf die glatte Fläche eines durchsichtigen Körpers wie FG fällt, im Einfallspunkte B so gebrochen wird, dass er mit der Geraden DBE, welche die Fläche senkrecht schneidet, einen Winkel CBE bildet, der kleiner ist als der Winkel ABD, den er mit derselben Senkrechten in der Luft bildete. Das Maass dieser Winkel findet man. wenn man um den Punkt B einen Kreis beschreibt, welcher die Strahlen AB und BC schneidet. Denn die von den Schnittpunkten auf die Gerade DE gefällten Senkrechten AD, CE, welche man die Sinus der Winkel ABD, CBE nennt, stehen unter sich in einem bestimmten Verhältniss, das bei allen Neigungswinkeln des einfallenden Strahles für ein und denselben Körper stets das nämliche ist. Beim Glase ist dies Verhältniss sehr nahe wie 3 zu 2 nnd beim Wasser nahezu wie 4 zu 3, und in ähnlicher Weise verschieden bei anderen durchsichtigen Körpern.

Eine andere, der vorstehenden ähnliche Eigenschaft besteht darin, dass die Brechungen der in einen durchsichtigen Körper eintretenden und antretenden Strahlen reciprok sind. Wenn nämlich der Lichtstrahl AB beim Eintritt in den durchsichtigen Körper sich in die Richtung BC bricht, so wird sich auch die Gerade CB, wenn man sie als einen Lichtstrahl im Innern dieses Körpers ansieht, beim Anstritt in die Richtung BA brechen.

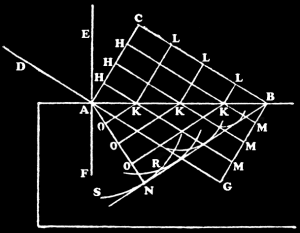Um nun diese Erscheinungen nach meinen Principien zu erklären, nehme ich an, dass die Gerade AB, welche eine Ebene darstellt, die durchsichtigen Körper begrenzt, welche nach C und N hin sich erstrecken. Wenn ich von einer Ebene spreche, so soll dies nicht eine vollkommene Ebene bezeichnen, sondern eine solche, wie sie oben bei der Besprechung der Reflexion gedacht worden ist, und zwar aus demselben Grunde. Die Linie AC möge einen Theil einer Lichtwelle darstellen, deren Mittelpunkt so entfernt angenommen wird, dass dieser Theil als eine gerade Linie angesehen werden kann. Die Stelle C der Welle A C wird nun in einem gewissen Zeiträume bis zur Ebene AB längs der Geraden CB gelangt sein, welche von dem leuchtenden Centrum ausgehend zn denken ist und darum A C rechtwinklig schneidet. In derselben Zeit würde nun die Stelle A längs der OB gleichen und parallelen Geraden A B in G angelangt sein, während der ganze Wellentheil AC in GB sein würde, wenn die Materie des durchsichtigen Körpers die Wellenbewegung ebenso schnell übertragen würde, wie diejenige des Aethers. [34] Nehmen wir jedoch an, dass sie diese Bewegung weniger schnell fortpflanze, beispielsweise um ein Drittel. Dann wird sich von dem Punkte A aus in dem Stoffe des durchsichtigen Körpers Bewegung ausgebreitet haben bis zu einer Erstreckung, welche 2/3 ist von CB, indem sie gemäss der früheren Auseinandersetzung ihre kugelförmige Einzelwelle bildet. Diese Welle wird demnach durch den Kreis SNR dargestellt, dessen Mittelpunkt A und dessen Halbmesser gleich 2/3 CB ist. Betrachtet man nunmehr die übrigen Stellen H der Welle AC, so ist klar, dass sie in derselben Zeit, in welcher die Stelle C nach B gelangt ist, nicht nur bis zu der Fläche AB durch die mit CB parallelen Geraden HK gelangt sein, sondern auch noch um die Mittelpunkte K Einzelwellen in dem durchsichtigen Körper erzeugt haben werden, welche hier durch Kreise dargestellt sind, deren Halbmesser gleich 2/3 der Linien KM sind, d. h. gleich 2/3 der Verlängerungen der HK bis zu der Geraden BG; denn diese Halbmesser würden den ganzen Strecken KM gleich gewesen sein, wenn die beiden durchsichtigen Mittel die nämliche Fortpflanzungsfähigkeit besässen.

Alle diese Kreise haben nun zur gemeinschaftlichen Tangente die Gerade BN, d. h. dieselbe, welche von B aus als Tangente an den zuerst betrachteten Kreis SNR gezogen ist. Denn es ist leicht einzusehen, dass alle übrigen Kreise ebenfalls BN berühren und zwar von B an bis zum Berührungspunkte N, welcher zugleich der Fusspunkt des Lothes AN auf BN ist.

Die Gerade BN also, welche gleichsam von kleinen Bogentheilchen dieser Kreise gebildet wird, begrenzt die Bewegung, welche die Welle AC an den durchsichtigen Körper mitgetheilt hat, und auf ihr ist diese Bewegung in grösserem Betrage vorhanden als überall sonstwo. Und darum ist diese Linie, wie bereits wiederholt dargelegt worden, die Fortsetzung der Welle AC in dem Augenblicke, in welchem ihre Stelle C in B angekommen ist. Denn es giebt unterhalb der Ebene AB keine andere Linie, welche wie BN die gemeinschaftliche Tangente aller jener Einzelwellen wäre. Will man [35] wissen, wie die Welle AC allmählich nach BN gelangt ist, so braucht man in derselben Figur nur die Geraden KO parallel zu BN und alle mit AC parallelen Linien KL zu ziehen. Die Welle CA wird also, wie man sieht, aus der Geraden in alle LKO nacheinander gebrochen und wird in B N wieder gerade. Da dies nach den früheren Darlegungen schon klar ist, bedarf es einer weiteren Erklärung nicht.

Zieht man nun in derselben Figur die Linie EAF, welche die Ebene AB im Punkt A rechtwinklig schneidet, und fällt man auf die Welle AC die Senkrechte AD, so wird DA den einfallenden Lichtstrahl und die auf BN senkrecht stehende AN den gebrochenen Strahl darstellen; denn die Lichtstrahlen sind nichts anderes als die geraden Linien, längs welcher die Theile der Wellen sich fortpflanzen.

Hieraus erkennt man leicht die Hauipteigenschaft der Brechung, nämlich dass der Sinus des Winkels DAE stets das nämliche Verhältniss zum Sinns des Winkels NAF hat, welches auch die Neigung des Strahles DA sein mag, und dass dies Verhältniss dasselbe ist, wie dasjenige der Geschwindigkeit der Wellen in dem gegen AE liegenden durchsichtigen Mittel zu ihrer Geschwindigkeit in dem durchsichtigen Mittel gegen AF. Denn betrachten wir AB als den Radius eines Kreises, so ist BC der Sinus des Winkels BAC und AN der Sinus des Winkels ABN. Der Winkel ABC ist aber gleich DAE; denn jeder von ihnen bildet, zu CAE hinzugefügt, einen rechten Winkel; und der Winkel ABN ist gleich NAF; denn jeder von ihnen bildet mit BAN [36] einen rechten Winkel. Der Sinus des Winkels DAE verhält sich also zu dem Sinus des Winkels NAF wie B C zu AN. Aber das Verhältniss von BC zu AN war dasselbe wie das der Lichtgeschwindigkeiten in den gegen AE und gegen AF hin gelegenen Materien; folglich muss sich auch der Sinus des Winkels DAE zum Sinus des Winkels NAF verhalten wie die genannten Lichtgeschwindigkeiten.